Curve di Cassini
Dimostrazione algebrica dell’equazione generica a cura di Roberto Spinelli
Nel tentativo di descrivere le orbite dei
pianeti intorno al sole, il matematico astronomo Giovanni Domenico Cassini
descrisse una famiglia di curve chiamate curve di Cassini. Partendo dalla
definizione di ellisse come luogo dei punti la cui somma delle distanze da due
punti fissi è costante si può pensare al luogo dei punti il cui prodotto delle
distanze da due punti fissi è costante. Partendo direttamente da quest’ultima
definizione possiamo arrivare all’equazione cartesiana generica di queste
curve.
Dati due punti detti fuochi 
e 
e considerando un punto generico P
poniamo
svolgendo i calcoli si ha
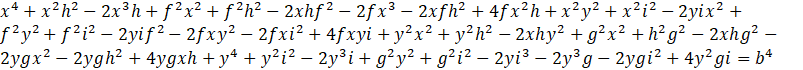
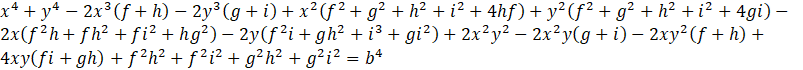
rinominiamo i coefficienti
L’equazione finale è:
Se i fuochi giacciono sull’asse x i valori g ed i sono nulli e si ha
(x2 + y 2 + c 2)2 −
4c 2x 2 = b 4
Al variare del rapporto b/c possiamo avere una curva ovale simile ad un’ellisse se b/c è maggiore di 1, una curva formata da due ovali che racchiudono i fuochi se b/c è minore di 1 oppure nel caso b/c=1 abbiamo una curva a forma di otto rovesciato che è il simbolo dell’infinito e si chiama “lemniscata di Bernoulli” dal nome del matematico Jakob Bernoulli che per primo ne studiò le proprietà.
Le curve di cassini come le coniche si possono ottenere nella geometria dello spazio come sezioni di un toro con un piano parallelo all’asse di rotazione, dalla distanza del piano dall’asse otteniamo i tre casi descritti in precedenza.